〈導入〉
y=ax+bについて学習した後、グラフの描き方やbの値が変わったときのグラフの特徴について考えます。
〈展開〉
①生徒は関数グラフツールを使ってy=2x+bの式について、bの値だけを変えてグラフを描きます。
②bの値を変えると、「原点を通っていない」「上下にbの値だけずれている」など、グラフにどのような影響があるのか考えます。
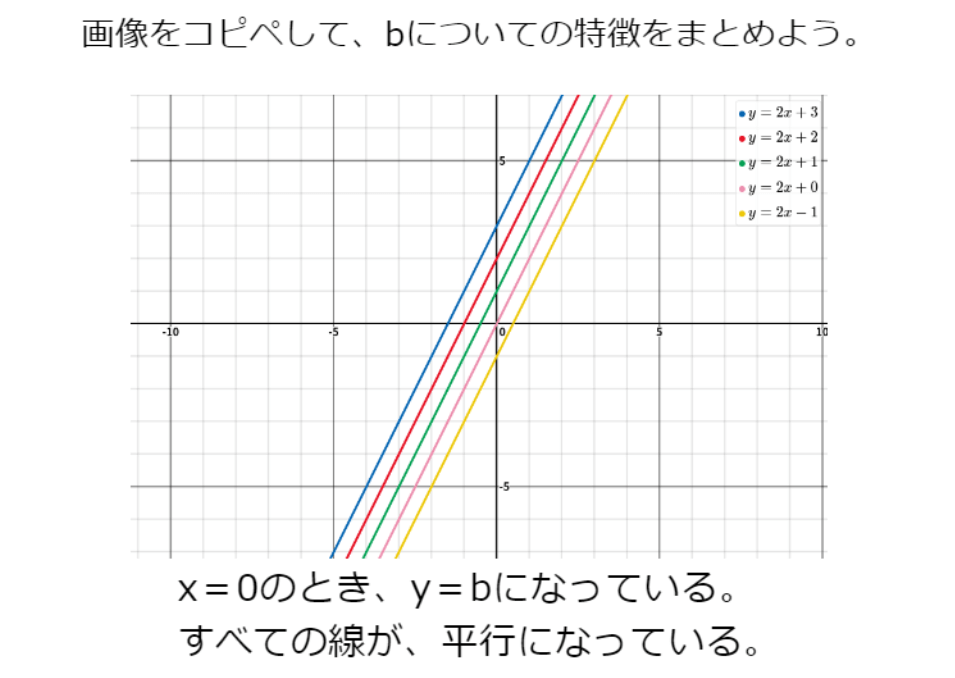
〈まとめ〉
y=ax+bのグラフについて、分かったことをまとめます。その後、実際にワークシート上に定規を使ってグラフを描く練習をします。

y=ax+bについて学習した後、グラフの描き方やbの値が変わったときのグラフの特徴について考えます。
①生徒は関数グラフツールを使ってy=2x+bの式について、bの値だけを変えてグラフを描きます。
②bの値を変えると、「原点を通っていない」「上下にbの値だけずれている」など、グラフにどのような影響があるのか考えます。

y=ax+bのグラフについて、分かったことをまとめます。その後、実際にワークシート上に定規を使ってグラフを描く練習をします。
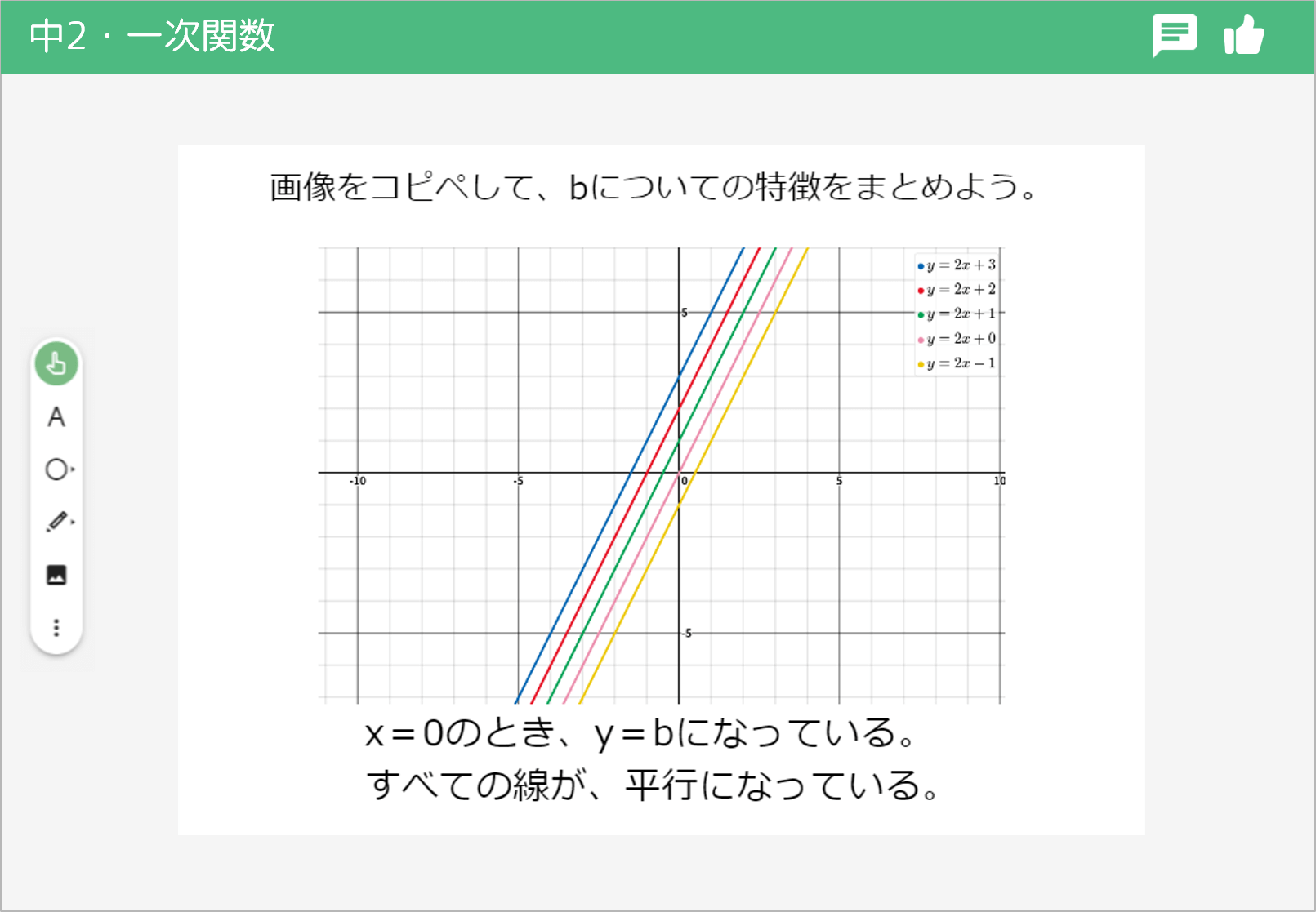
一次関数の式における、b(切片)の値が、グラフにどのように影響するのかを発見するために、スクールタクトの関数グラフツールを活用しました。
関数グラフツールは、式を入力するとグラフを簡単に描画できます。複数の式を入力することで並べて比較することができるので、bの値によってどのようにグラフが変わっているのか、理解しやすかったです。
関連するコンテンツはありません。